Giới thiệu độ phức tạp của thuật toán Big O

1. Giới thiệu

Tại sao phải tối ưu hóa độ phức tạp của thuật toán?

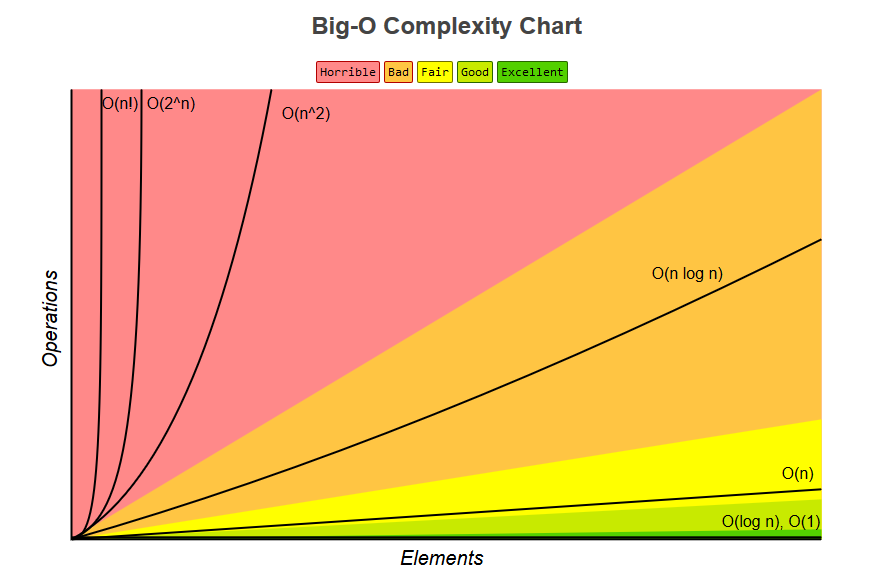
Figure 1: Big O

Đơn giản vì độ phức tạp thấp thì sản phẩm của bạn sẽ chạy mượt mà hơn.

Độ phức tạp của thuật toán phụ thuộc vào mối quan hệ giữa số lượng phép tính cần thực hiện và số lượng đầu vào của hàm số.

2. Ví dụ

bigO.py

import time
start = time.time()
i = 0
n = 1000000

while i < n:
    print(i)
    i += 1

print("time: " +  str(time.time() - start))

Đối với đoạn code trên thì $P(n)=3n+2 \sim O(n)$

Tại sao lại tính được như vậy?

bigO_2.py

import time
start = time.time()
i = 0 # phep gan +1
n = 1000000 # phep gan +1

while i < n: # phep so sanh +1
    print(i) # +1
    i += 1   # +1

# while n buoc -> (1+1+1)xn = 3n -> 3n + 2

print("time: " +  str(time.time() - start))

Thật dễ để hiểu đúng không?

Đến với vị dụ tiếp theo:

bigO_3.py

n = 10
x = 1
y = 2
# +3
for i in range(n): # phep so sanh i < n ? va phep i++ => +2
    for j in range(n): # phep so sanh j < n ? va phep j++ => +2
        x = x + 1 # +1
        y = y + 1 # +1
        # => 4n + 2
# => (4n + 2)xn
# => P(n) = 4n^2 + 2n + 3
# => O(n^2)

$P(n) = 4n^2 + 2n + 3 \sim O(n^2)$

Đối với đoạn code dưới đây thì sao?

bigO_4.py

n = 10
x = 1
y = 2
i = 1
# +4
while i < n: # phep so sanh +1 
    x = x + 1 # +1
    i *= 2 # +1
    print(x)

Do i *= 2 nên vòng while không duyệt $n$ lần mà duyệt $log_2(n)$
$P(n) = 3\log_{2}(n) + 4 \sim O(log_2(n))$

NOTE

To be updated